บทที่ 3/2 ความน่าจะเป็น

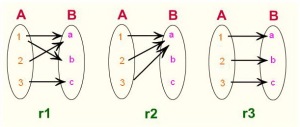
        ความน่าจะเป็น คือ ค่าที่ใช้ประเมินสถานการณ์ที่ยังไม่เกิดขึ้น โดยพิจารณาว่า เมื่อถึงเวลาเกิดเหตุการณ์แล้ว จะเกิดในลักษณะใด มีโอกาสที่จะเกิดมากน้อยเพียงใด การหาค่าความน่าจะเป็น จะต้องหาจากการทดลองสุ่มเท่านั้น

แซมเปิลสเปซ (Sample Space )
แซมเปิลสเปซ คือเซตของเหตุการณ์ทั้งหมดจากการทดลอง (Universal Set) เช่น การโยนลูกเต๋าถ้าต้องการดูว่าหน้าอะไรจะขึ้นมาจะได้ S = { 1, 2, 3  อ่านเพิ่มเติม

บทที่ 2/2 อัตราส่วนตรีโกณมิติ

คำว่า “ตรีโกณมิติ” ตรงกับคำ ภาษาอังกฤษ “Trigonometry” หมายถึง การวัด รูปสามเหลี่ยมได้มีการนำความรู้วิชาตรีโกณมิติไปใช้ในการหาระยะทาง พื้นที่ มุม และทิศทางที่ยากแก่การวัดโดยตรง เช่น การหาความสูงของภูเขา การหาความกว้างของแม่น้ำ เป็นต้น              จากรูปสามเหลี่ยมมุมฉาก ABC ที่มีมุม C เป็นมุมฉาก

เมื่อพิจารณามุม A

BC เรียกว่า ด้านตรงข้ามมุม A ยาว a หน่วย

CA เรียกว่า ด้านประชิดมุม  อ่านเพิ่มเติม

บทที่ 1/2 เลขยกกำลัง

1.รากที่ n

        ในทางคณิตศาสตร์ รากที่ n ของจำนวน x คือจำนวน r ที่ซึ่งเมื่อยกกำลัง n แล้วจะเท่ากับ x นั่นคือ

        ตัวแปร n คือจำนวนที่ใส่เข้าไปเป็นดีกรีของราก โดยทั่วไปรากของดีกรี n จะเรียกว่ารากที่ n เช่นรากของดีกรีสองเรียกว่า

รากที่สอง รากของดีกรีสามเรียกว่ารากที่สาม เป็นอาทิ

ตัวอย่างเช่น

        2 คือรากที่สองของ 4  อ่านเพิ่มเติม

...........................................................................................................................

2. เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ      

                

            บทนิยาม   กำหนดให้  a เป็นจำนวนจริง  n  เป็นจำนวนเต็มที่มากกว่า  1

และ  รากที่ n ของ a  เป็นจำนวนจริง  จะได้ว่า aยกกำลัง1 ส่วน n=รากที่ aของ n

บทนิยาม        ให้ m ,n  เป็นจำนวนเต็มบวก ถ้า a  เป็นจำนวนจริงที่ไม่เท่ากับ 0

และ  หาค่า     = aยกกำลังลบmส่วนn = 1ส่วนaยกกำลังmส่วนn

บทนิยาม        ให้  a  เป็นจำนวนจริง

m และ  n  เป็นจำนวนเต็มที่  n >  o  และ  mส่วนn  เป็นเศษส่วนอย่างต่ำ  จะได้ว่า

aยกกำลังmส่วนn  =   aยกกำลัง1 อ่านเพิ่มเติม

บทที่ 4/1 ความสัมพันธ์และฟังก์ชัน

คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง

(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d

ผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B

สัญลักษณ์      ผลคูณคาร์ทีเซียนของเซต A และเซต B เขียนแทนด้วย A x B
หรือ เขียนในรูปเซตแบบบอกเงื่อนไขจะได้ว่า 

ความสัมพันธ์ (Relation)
r เป็นความสัมพันธ์จาก A ไป B  อ่านเพิ่มเติม

บทที่ 3/1 จำนวนจริง

จำนวนจริง

เซตของจำนวนจริงประกอบด้วยสับเซตที่สำคัญ  ได้แก่

- เซตของจำนวนนับ/ เซตของจำนวนเต็มบวก เขียนแทนด้วย  I

                   I = {1,2,3…}

- เซตของจำนวนเต็มลบ  เขียนแทนด้วย  I

- เซตของจำนวนเต็ม เขียนแทนด้วย I

                   I = { …,-3,-2,-1,0,1,2,3…}

- เซตของจำนวนตรรกยะ : เซตของจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วน      โดยที่ a,b เป็นจำนวนเต็ม  และ b = 0

NOTE จำนวนต่อไปนี้เป็น จำนวนตรรกยะ 1.            จำนวนเต็ม ได้แก่ 0,1,-1,2,-2,3,-3,... 2.            จำนวนที่เขียนในรูปเศษส่วนของจำนวนเต็มและตัวส่วนไม่เป็นศูนย์  เช่น 3.            จำนวนที่เขียนในรูปทศนิยมซ้ำ เช่น 1.414 , -0.17 , 1.508

- เซตของจำนวนอตรรกยะ : จำนวนที่ไม่ใช่จำนวน อ่านเพิ่มเติม

บทที่ 2/1 การให้เหตุผล

1.การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เกิดจากการที่มีสมมติฐานกรณีเฉพาะ หรือเหตุย่อยหลายๆ เหตุ เหตุย่อยแต่ละเหตุเป็นอิสระจากกัน มีความสำคัญเท่าๆ กัน และเหตุทั้งหลายเหล่านี้ไม่มีเหตุใดเหตุหนึ่งแสดงให้เห็นถึงความเป็นสมมติฐานกรณีทั่วไป หรือกล่าวได้ว่า การให้เหตุผลแบบอุปนัยคือการนำเหตุย่อยๆ แต่ละเหตุมารวมกัน เพื่อนำไปสู่ผลสรุปเป็นกรณีทั่วไป เช่นตัวอย่างการให้เหตุผลแบบอุปนัย

         1. สุนทรี พบว่า ทุกครั้งที่คุณแม่ไปซื้อก๋วยเตี๋ยวผัดไทยจะมีต้นกุยช่ายมาด้วยทุกครั้ง  จึงสรุปว่า ก๋วยเตี๋ยวผัดไทยต้องมีต้นกุยช่าย

         2.ชาวสวนมะม่วงสังเกตมาหลายปีพบว่า ถ้าปีใดมีหมอกมาก ปีนั้นจะได้ผลผลิตน้อย เขาจึงสรุปว่าหมอกเป็นสาเหตุที่ทำให้ผลผลิตน้อย ต่อมามีชาวสวนหลายคนทดลองฉีดน้ำล้างช่อมะม่วง เมื่อมีหมอกมากๆ พบว่าจะได้ผลผลิตมากขึ้นจึงสรุปว่า การล้างช่อมะม่วงตอนมีหมอกมากๆ จะทำให้ได้ผลผลิตมากขึ้น

         3.นายสมบัติ พบว่า ทุกครั้งที่ทำความดีจะมีคว อ่านเพิ่มเติม

.........................................................................................................................

2.การให้เหตุผลแบบนิรนัย

                การให้เหตุผลแบบนิรนัยเป็นวิธีการให้เหตุผลโดยสรุปผลจากข้อความซึ่งเป็นความจริงทั่วไปมาเป็นข้ออ้างเพื่อสนับสนุนให้เกิดข้อสรุปที่เป็นความรู้ใหม่ที่เป็นข้อสรุปส่วนย่อยข้อสรุปที่ได้จากการให้เหตุผล

แบบนิรนัยนั้นจะเป็นข้อสรุปที่อยู่ในขอบเขตของเหตุเท่านั้นจะเป็นข้อสรุปที่กว้างหรือเกินกว่าเหตุไม่ได้การให้เหตุผลแบบนิรนัยประกอบด้วยข้อความ2กลุ่มโดยข้อความกลุ่มแรกเป็นข้อความที่เป็นเหตุ เหตุอาจมีหลาย ๆเหตุ หลาย ๆข้อความ และข้อความกลุ่ อ่านเพิ่มเติม

บทที่ 1/1 เซต

เซต  เป็นคำที่ใช้บ่งบอกถึงกลุ่มของสิ่งต่างๆ และเมื่อกล่าวถึงกลุ่มใดแน่นอนว่าสิ่งใดอยู่ในกลุ่ม สิ่งใดไม่อยู่ในกลุ่ม เช่น

       เซตสระในภาษาอังกฤษ  หมายถึง  กลุ่มของอังกฤษ  a, e, i, o และ u

       เซตของจำนวนนับที่น้อยกว่า 10 หมายถึง  กลุ่มตัวเลข 1,2,3,4,5,6,7,8,และ9

        สิ่งที่ในเชตเรียกว่า  สมาชิก  ( element หรือ members )

การเขียนเซต

การเขียนเซตอาจเขียนได้ 2  แบบ

   1 การเขียนซตแบบแจกแจงสมาชิก  เขีย อ่านเพิ่มเติม